From the above video, try to identify what are the image processing and computer vision methods used in the applications explained by the speaker.
Call for Ph.D./Master Student
This year we manage to secure a research grant. Thus, anyone interested to join us, please contact me as soon as possible. Below is the flyer for more info. Also, please distribute to those who might be interested.

Image Processing VS Computer Vision
Class for the semester 20192020-1 starts this week. Let us overview some fact about image processing to start the course.

See more graphical notes here.
New Update on the DSP Concept Mapping
This is a small update and amendment to the DSP Concept Mapping chart. And I also change it to the dark theme.

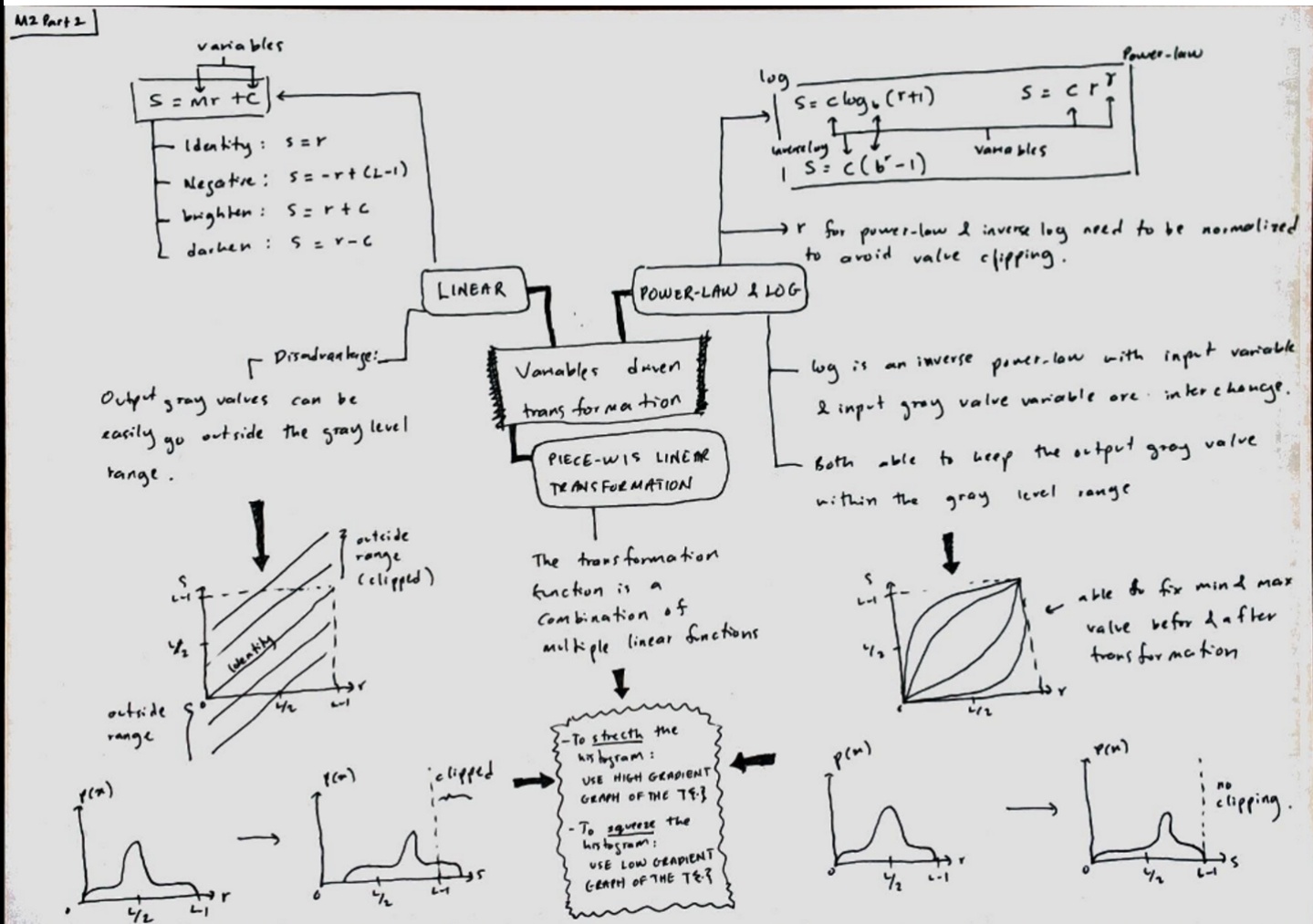
Visual Note on Variable Driven Transformation is Complete
Check out the new visual note. This is part of the content from the Image Processing course, chapter 2.

Click here for more visual note
Visual Note: Variable Driven Point Processing
Quotes of the day
It is literally true that you can succeed best and quickest by helping others to succeed
Napolean Hill
Quotes of the Day
If everybody is thinking alike, then somebody isn’t thinking
Quotes of the Day
I don’t want to talk, to communicate, with someone who agrees with me. I want to communicate with you because you see it differently.
Covey, 1990
Kaedah Darab KAH
Kontroversi operasi darab 2×5 yang dikatakan tidak sama dengan 5×2 adalah kisah lama. Tetapi oleh kerana terjumpa semula dokumen berkaitan perkara ini, berikut ialah pendapat saya.
Kaedah KAH (Kumpulan, ahli dan Hasil) dipercayai dapat memudahkan pemahaman anak-anak untuk membina ayat matematik darab sekaligus melaksanakan operasi tersebut. Untuk membina ayat matematik, kaedah KAH memerlukan kita mengenalpasti kumpulan terlebih dahulu, kemudian jumlah ahli dalam setiap kumpulan dan akhirnya jumlah hasil darab. Kita mulakan dengan contoh pertama seperti di Gambarajah 1.

KUMPULAN boleh ditafsirkan sebagai kelompok objek yang mempunyai ciri yang sama. Merujuk kepada Gambarajah 1 di atas, ciri yang paling jelas dikongsi oleh peserta ialah nama PASUKAN di mana 5 peserta berada di Pasukan A dan 5 peserta berada di Pasukan B. Selain pasukan, kumpulan juga boleh dibina dari ciri JANTINA dan NEGERI. Untuk kumpulan Jantina, terdapat 5 peserta lelaki dan 5 peserta perempuan manakala untuk kumpulan Negeri, terdapat 2 peserta untuk setiap 5 negeri.
Oleh itu terdapat 3 KAH yang boleh dibina daripada gambarajah di atas iaitu:
KAH Pasukan: 2 x 5 = 10
2 kumpulan PASUKAN (A dan B). Setiap PASUKAN ada 5 ahli.
KAH Jantina: 2 x 5 = 10
2 kumpulan JANTINA (lelaki dan perempuan). Setiap JANTINA ada 5 ahli.
KAH Negeri: 5 x 2 = 10
5 kumpulan KUMPULAN (Selangor, Sabah, Sarawak, Pahang dan Perak). Setiap NEGERI ada 2 ahli.
Sekarang kita beralih kepada situasi kedua seperti yang tertera pada Gambarajah 2. Cuba perhatikan apakah jenis kumpulan yang boleh dikenalpasti.

Sekali lagi kumpulan yang paling ketara adalah PASUKAN di mana terdapat 2 pasukan iaitu A dan B. Melihat kepada contoh pada Gambarajah 1 sebelum ini, Gambarah 2 juga mempunyai kumpulan berdasarkan JANTINA. Tetapi kali ini terdapat hanya satu jantina sahaja iaitu lelaki. Ini berbeza dengan kumpulan NEGERI di mana ianya tidak wujud sama sekali untuk contoh pada Gambarajah 2.
Apa yang tidak dapat dilihat tetapi wujud daripada Gambarajah 2 adalah pernomboran kepada setiap ahli pasukan seperti yang ditunjukkan pada Gambarajah 3 di bawah. Pernomboran ini boleh wujud daripada nombor yang diberikan semasa mengisi nama ahli kumpulan atau nombor giliran menjawab soalan jika ianya adalah pertandingan kuiz antara 2 pasukan tersebut. Pernomboran ini juga boleh diistilahkan sebagai INDEX.

Oleh itu, INDEX juga merupakan sejenis kumpulan dimana terdapat 2 peserta untuk setiap 5 Index pasukan. Dan tidak mustahil jika setiap peserta tidak mengira pasukan diindex dengan nombor yang berlainan. Maka akan wujud satu ahli untuk 10 kumpulan INDEX.
Berikut adalah ayat matematik darab untuk contoh kali ini:
KAH Pasukan: 2 x 5 = 10
2 kumpulan PASUKAN (A dan B). Setiap PASUKAN ada 5 ahli.
KAH Jantina: 1 x 10 = 10
1 kumpulan JANTINA (lelaki). Setiap JANTINA ada 10 ahli.
KAH Index Pasukan: 5 x 2 = 10
5 kumpulan INDEX PASUKAN (1, 2, 3, 4 dan 5). Setiap INDEX PASUKAN ada 2 ahli.
KAH Index Peserta: 10 x 1 = 10
10 kumpulan INDEX PESERTA (1, 2, 3, 4, 5, 6, 7, 8, 9 dan 10). Setiap INDEX PESERTA ada 1 ahli.
Kesimpulannya, kesemua ayat matematik darab di atas boleh digunakan untuk contoh kali ini. Ini dibuktikan dengan jumlah hasil kesemua ayat matematik darab tersebut adalah sama iaitu 10.
Sebagai latihan, cuba kenalpasti jenis-jenis kumpulan dan bilangan ahli setiap kumpulan untuk gambar seterusnya (Gambarajah 4). Kemudian bina ayat matematik darab untuk mendapatkan jumlah keseluruhan brownies.

Cuba juga kenalpasti 2 lagi kumpulan untuk contoh pertama pada Gambarajah 1. Selamat mencuba.