1D Shape Function
clear, clc
syms x
q = 2; %order of poly (eg. quad–> q=2)
L = 1;
%create ux = a1 + a2x + …
A1 = []; A0 = []; %temporary variables
ux = 0;
for i = 1:q+1
aN = [‘a’ num2str(i)];
syms(aN);
ux = ux + aN*x^(i-1);
A0 = cat(2,A0,[aN,’,’]);
A1 = cat(2,A1,sym(aN));
end
%use EBC to obtain sufficient simultaneous eqs
X = 0:L/q:L;
for i = 1:length(X)
eqns(i) = sym(subs(ux,x,X(i)) == [‘u’ num2str(i)]);
end
%solve the simultaneous eqs
A2 = solve(eqns,A1);
%convert to ux = Ni*ui
A3 = expand(subs(ux,A1,struct2array(A2)));
U1 = []; %temporary variable
for i = 1:q+1
uN = [‘u’ num2str(i)];
syms(uN);
A3 = collect(A3,uN);
U1 = cat(2,U1,sym(uN));
end
%get the SF and their derivative
SF = coeffs(A3,U1(end:-1:1))
dSF = diff(SF)
fplot(SF,[0 L])
2D Shape Function
clear, clc
syms x y E v
syms a1 a2 a3 a4 T1 T2 T3 T4 real
a = 1;
b = 1;
%assumed solution
Txy = a1 + a2*x + a3*y + a4*x*y;
%obtain equations
eq1 = subs(Txy,[x y],[0 0]) == T1;
eq2 = subs(Txy,[x y],[a 0]) == T2;
eq3 = subs(Txy,[x y],[a b]) == T3;
eq4 = subs(Txy,[x y],[0 b]) == T4;
%solve simultaneous equations
A = solve([eq1,eq2,eq3,eq4],a1,a2,a3,a4);
a1 = A.a1;
a2 = A.a2;
a3 = A.a3;
a4 = A.a4;
%substitute back & rearrange
Txy = a1 + a2*x + a3*y + a4*x*y;
Txy = expand(Txy);
Txy = collect(Txy,[T1,T2,T3,T4])
%determine SF
[N,Ti] = coeffs(Txy,[T1,T2,T3,T4]);
N1 = N(1)
N2 = N(2)
N3 = N(3)
N4 = N(4)
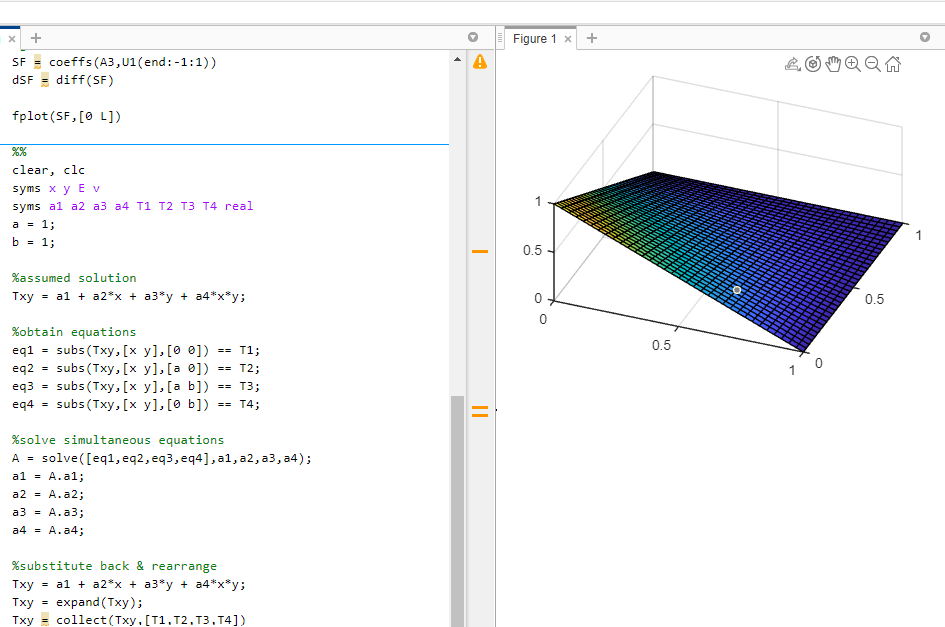
fsurf(N1,[0 a 0 b])


Recent Comments