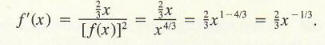Finding the derivative of
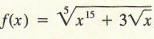
involves computing the following limit:
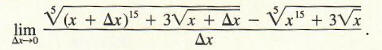
To put it mildly, this calculation would be unpleasant. We would like to find ways to compute derivatives without explicitly using the definition of the derivative as the limit of a difference quotient. A useful preliminary result is the following:
Derivative of a Constant
lf c is any real number and if f(x) = c for all x, then f ‘ (x) = 0 for all x . That is, the derivative of a constant function is the zero function.
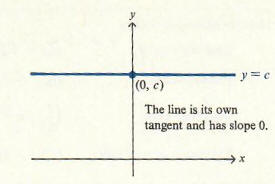
It is easy to see this geometrically. Referring to Figure 1, we see that the graph of the constant function f(x) = c is a horizontal line. Since a horizontal line has slope 0, and the line is its own tangent, it follows that the slope of the tangent line is zero everywhere. We next give a rule for differentiating f(x) = xn where n is any real number. Some of the following results have already been verified in the previous section, and the others can be verified by using the definition of the derivative.
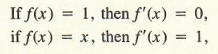
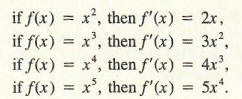
This pattern suggests the following general formula for powers of n where n is a positive integer.
Power Rule

In fact, the power rule is valid for any real number n and thus can be used to differentiate a variety of non-polynomial functions. The following example illustrates some applications of the power rule.
Example 1 Differentiate each of the following functions:
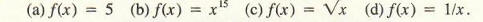
(a) Since f(x) = 5, f is a constant function; hence f ‘(x) = 0.
(b) With n = 15 in the power rule, f ‘(x) = 15x14
(c) Note that f(x) = x1/2 . Hence, with n = 1/2 in the power rule,
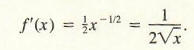
(d) Since f(x) = x-1, it follows from the power rule that f ‘(x) = -x-2 = -1/x2
The rule for differentiating constant functions and the power rule are explicit differentiation rules. The following rules tell us how to find derivatives of combinations of functions in terms of the derivatives of their constituent parts. In each case, we assume that f ‘(x) and g'(x) exist and A and B are constants.
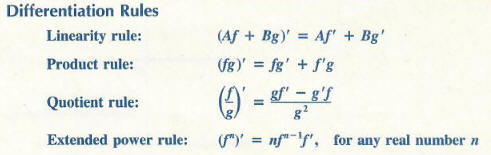
The four rules listed above, together with the rule on differentiating constant functions and the power rule, provide us with techniques for differentiating any function that is expressible as a power or root of a quotient of polynomial functions. The next series of examples illustrates this. The linearity rule and the product rule will be justified at the end of the section; a proof of the extended power rule appears in the section on the chain rule.
Example 2 Let
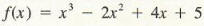
Find f ‘(x). Solution Using the linearity rule, we see that
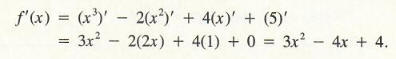
Example 3 Let
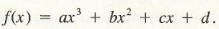
Again using linearity,
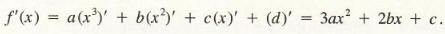
f'(x) = a(x3)’ + b(x2)’ + c(x)’ + (d)’ = 3ax^2 + 2bx + c
Example 3 can be generalized as follows:
A polynomial of degree n has a derivative everywhere, and the derivative is a polynomial of degree (n – 1).
Example 4 Let
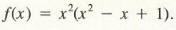
Find f ‘(x).
First we use the product rule, since f(x) is given as the product of x2 and x2 – x + 1:
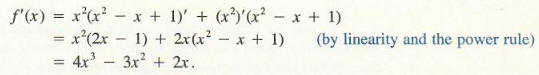
The equation y = x2 + 1 explicitly defines y as a function of x, and we show this by writing y = f (x) = x2 + 1. If we write the equation y = x2 + 1 in the form y – x2 – 1 = 0, then we say that y is implicitly a function of x. In this case we can find out what that function is explicitly simply by solving for y. Sometimes, however, we must deal with equations relating y to x that are so complicated that it is difficult or even impossible to solve for y in terms of x. (For example, try to solve for yin the equation yy+ xy = 10.) If an equation implicitly defines y as a function of x, there is a way to find dy/dx without first explicitly finding y as a function of x, called implicit differentiation.
We will use the equation y – x2 – 1 = 0 to illustrate this technique. Instead of explicitly solving for y, assume that it would be possible to solve for y in terms of x; call the resulting function y(x) for simplicity. The equation can now be written as
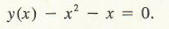
Differentiating both sides with respect to x by means of the sum and power rules, we obtain
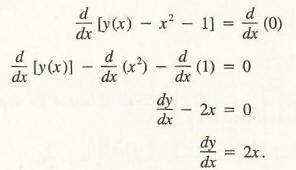
This same result would be obtained by solving for y so that y = x2 + 1, from which dy/dx = 2x. In this example it is easier to first solve for y and then differentiate, but this will not always be the case.
Example 1
Find the slope of the tangent line to the graph of the equation xy – x = 1 at that point on the graph whose first coordinate is 1 (that is, corresponding to x = 1).
Solution
We must find dy/dx at x = 1. Assume y is a function of x, y = y(x). The relation now is xy(x) – x = 1.
Hence,
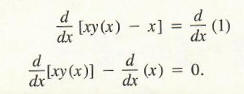
and by the extended power rule,
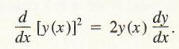
Substituting these results into Formula (2), we obtain
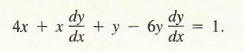
We solve this equation for dy/dx:
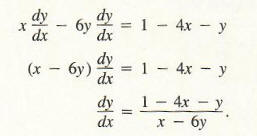
Be careful! When applying Formula (3), keep in mind that the only values of x and y that can be substituted into the right-hand side of Formula (3) are those values that satisfy the original condition 2x2 + xy – 3y2 = x. For instance, we might substitute x = 1, y = 4 to obtain (dy/dx) = (1 – 4 – 2)/(1 – 12) = 5/1; however, (1, 2) is not a point on the graph of 2x2 + xy – 3y2 = x, so the calculation of dy/dx at this point is totally meaningless.
The equation in Example 2 can be written as – 3y2 + xy + (2x2 – x) = 0 and hence is a quadratic equation in y (an equation of the form Ay2 + By + C = o where A = -3, B = x and C = 2x2 – x). Hence, we could use the quadratic formula to solve this equation for y in terms of x, obtaining
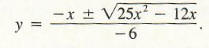
Though we are able to find y explicitly in terms of x , the resulting expression is fairly complex, and it still might be best to find dy/dx implicitly as in Example 2.
Example 3 Find dy/dx if y4 + xy = 10.
Solving for y in terms of x is difficult if not impossible in this problem. However, by implicit differentiation, we obtain
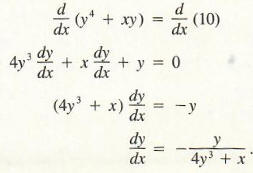
The following example illustrates how implicit functions can be used to justify the fact that dxn /dx = nxn-1 i is valid when n is a rational number.
Example 4 Let f(x) = x2/3. Use implicit differentiation to show that
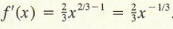
Since f(x) = x2/3 , we obtain, by cubing, [f(x)]3 = x2.
Differentiate with respect to x.
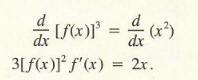
Hence,